○ 진단(diagnosis) : 회귀분석에 사용된 데이터가 회귀분석에 사용된 모형 가정을 제대로 만족하고 있는지를 확인하는 과정
○ 잔차 정규성 : 데이터가 모형 가정을 만족하면 분석결과로 나온 잔차는 정규분포를 따라야 한다.


○ 잔차와 독립 변수 : 데이터가 올바른 모형으로 분석되었다면 잔차는 더이상 독립 변수와 상관관계를 가지지 않아야 한다.


○ 이분산성 : 선형 회귀 모형에서는 종속 변수 값의 분산이 독립 변수의 값과 상관없이 고정된 값을 가져야한다. 그러나 실제 데이터는 독립 변수 값의 크기가 커지면 종속 변수 값의 분산도 커지는 이분산성(heteroskedastic) 문제가 발생한다.

○ 자기 상관 계수 : 선형 회귀 모형에서는 오차(disturbance)들이 서로 (모수-조건부) 독립이라고 가정하고 있다. 따라서 잔차(residual)도 서로 독립이어야 한다. 오차가 독립인지 검정하는 방법은 잔차를 시계열로 가정하여 자기상관계수를 구하는 것이다.
○ 비선형 변형 : 만약 독립변수와 종속변수간의 관계가 비선형이면 이 관계를 선형으로 바꿀 수 있도록 독립변수를 비선형 변환할 수 있다.





○ 독립변수의 비선형성을 포착하는 또 다른 방법 중 하나는 강제로 범주형 값으로 만드는 것이다.



○ 시간 독립변수의 변형 : 독립변수가 시간인 경우에는 특정 시점에서 경과된 시간값으로 변형해야 한다.

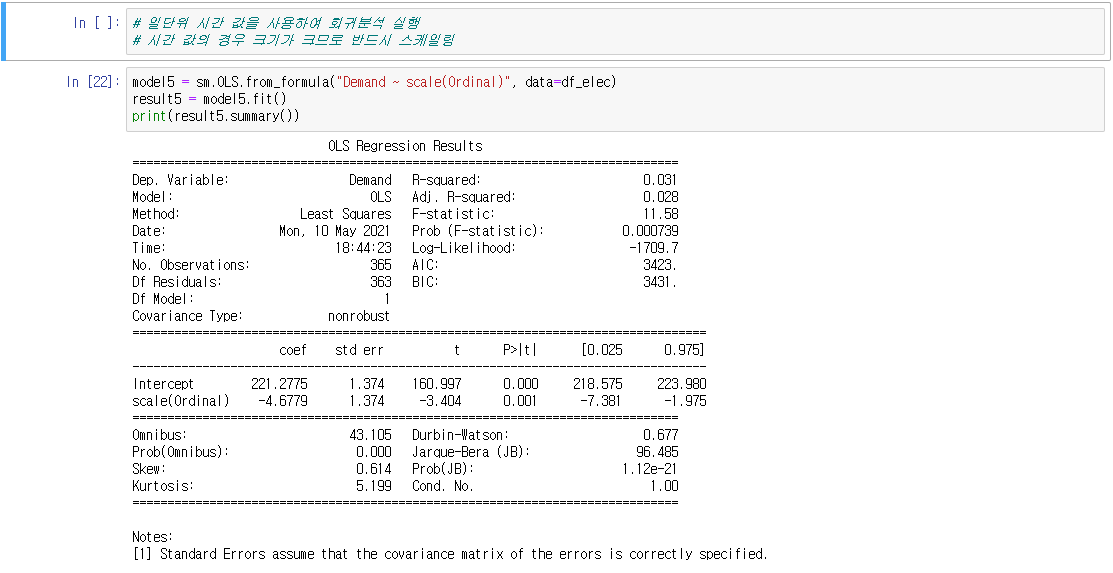
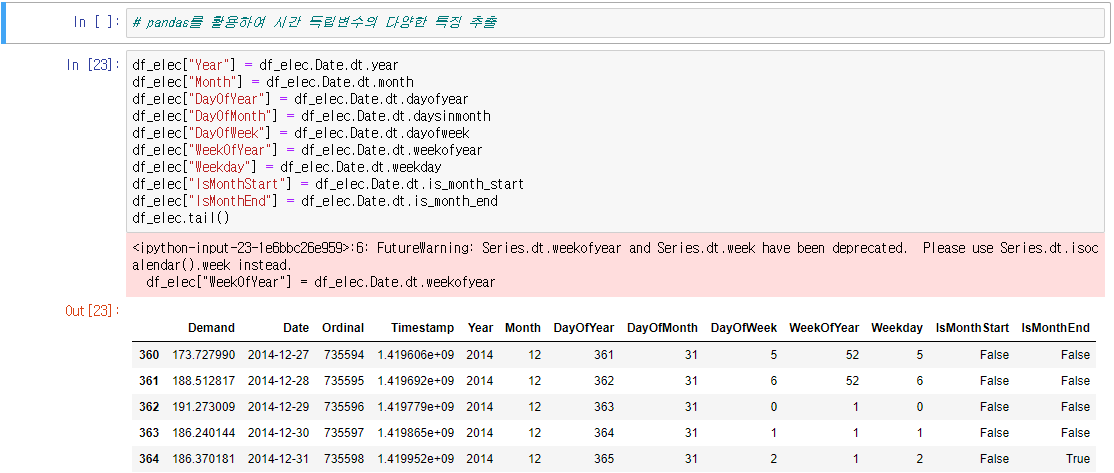
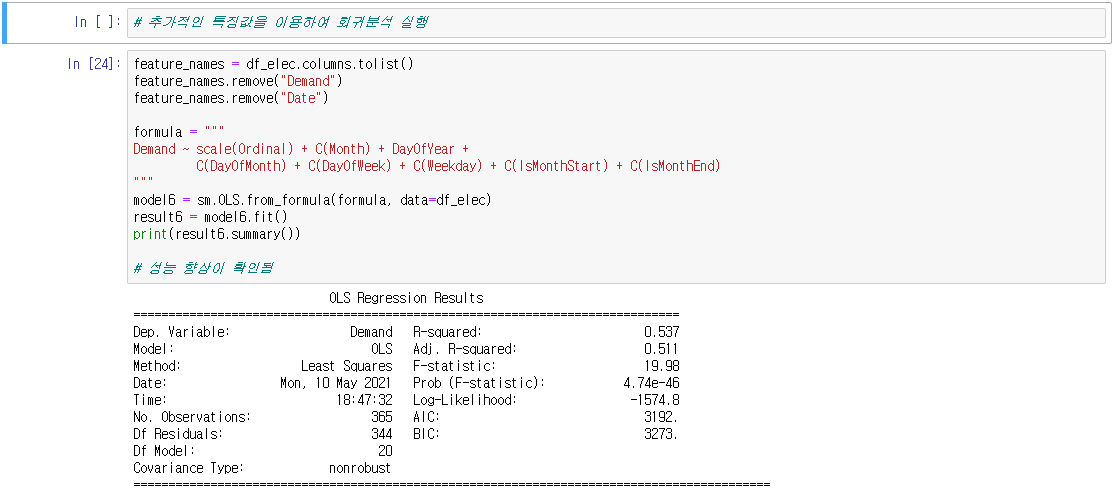

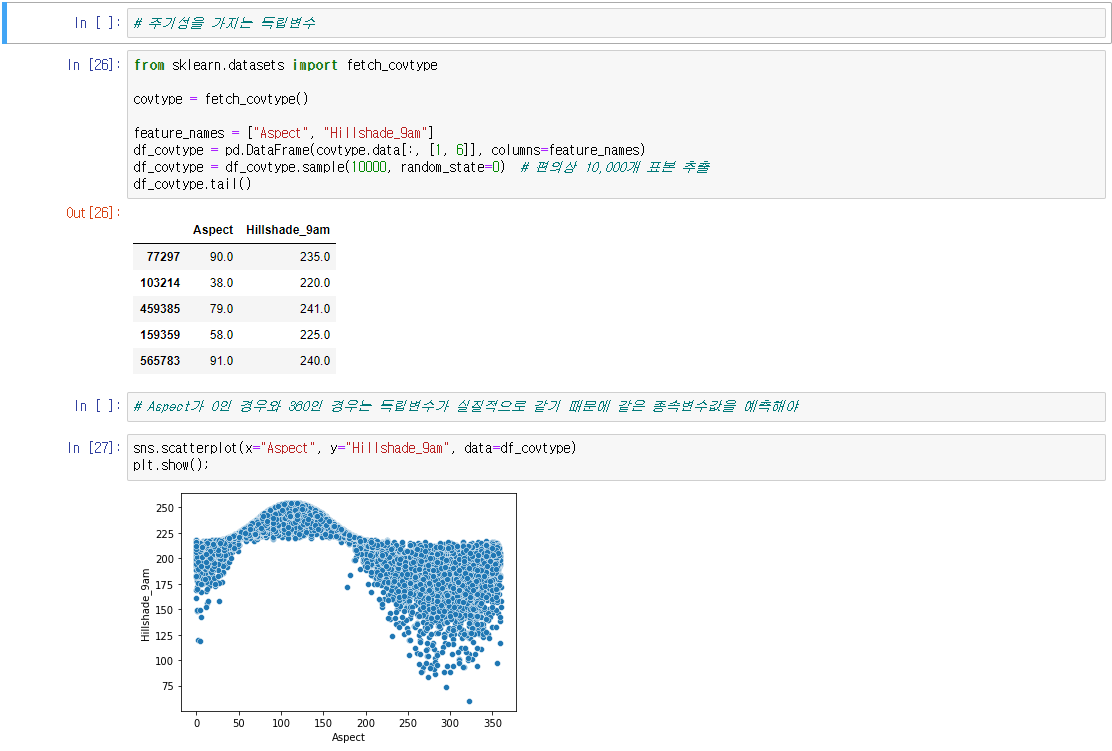
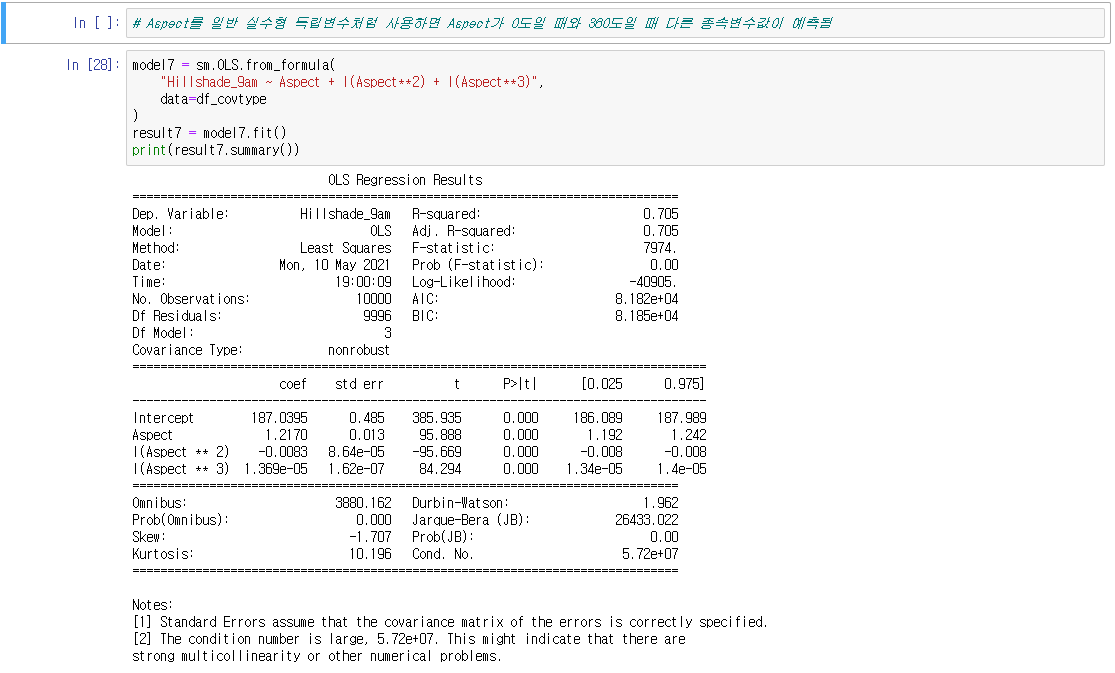
○ 주기성을 가지는 독립변수 : 독립변수가 주기성을 가지는 경우에는 그대로 사용하면 모형이 주기성을 가지지 못한다.



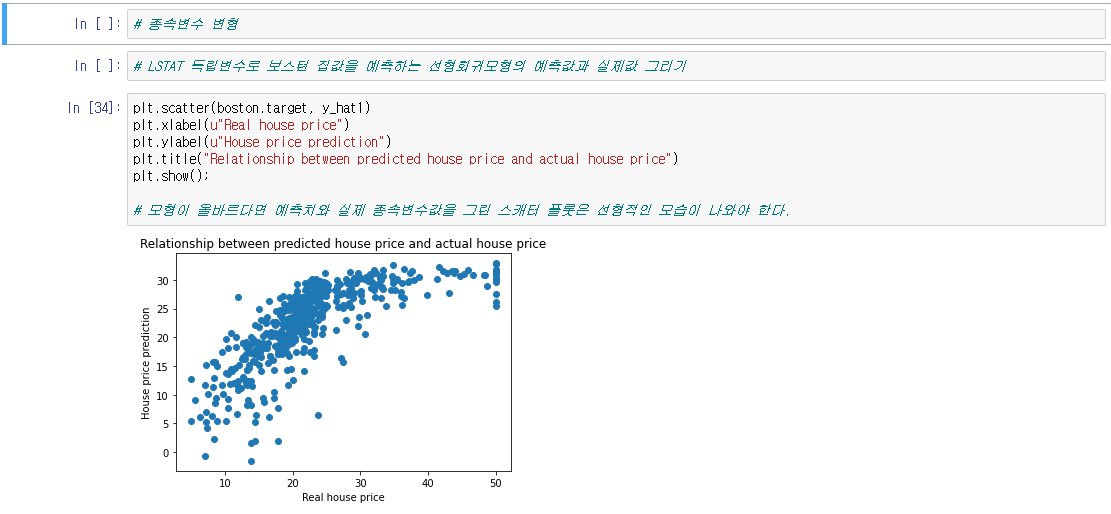
○ 종속변수 변형 : 경우에 따라서는 종속변수를 변형할 수도 있다.


- 출처 : [데이터 사이언스 스쿨] 6.1 모형 진단과 수정
'IT 와 Social 이야기 > Python' 카테고리의 다른 글
| [데이터 사이언스 스쿨] 6.3 교차검증 cross validation (0) | 2021.05.11 |
|---|---|
| [데이터 사이언스 스쿨] 6.2 기저함수 모형과 과최적화 (0) | 2021.05.11 |
| [데이터 사이언스 스쿨] 5.4 분산 분석과 모형 성능 ANOVA (0) | 2021.05.10 |
| [데이터 사이언스 스쿨] 5.3 레버지리와 아웃라이어 (0) | 2021.05.10 |
| [데이터 사이언스 스쿨] 5.1 확률론적 선형 회귀모형 probabilistic model (0) | 2021.05.10 |



