



● 스칼라와 벡터의 곱
양의 실수와 벡터를 곱하면 벡터의 방향은 변하지 않고 실수의 크기만큼 벡터의 길이가 커진다. 만약 음의 실수를 곱하면 벡터의 방향이 반대가 된다.

● 벡터의 합
벡터와 벡터의 합도 벡터가 된다. 이때 두 벡터의 합은 그 두 벡터를 이웃하는 변으로 가지는 평행사변형의 대각선 벡터가 된다.

● 벡터의 선형조합
여러 개의 벡터를 스칼라곱을 한 후 더한 것


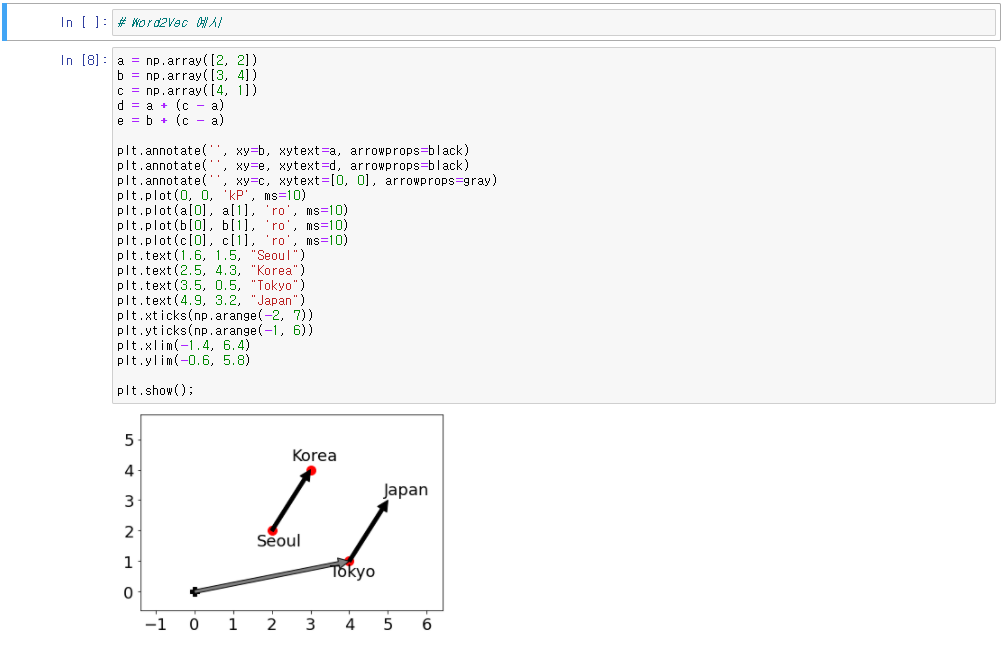
● Word2Vec 예시
● 벡터의 내적과 삼각함수
두 벡터의 내적은 두 벡터 사이의 각도 θθ의 코사인 함수값으로 계산할 수도 있다.

dss_math3_1_linear algebra vs geometry.ipynb
0.13MB
'IT 와 Social 이야기 > Python' 카테고리의 다른 글
| [데이터 사이언스 스쿨] math 3.3 고윳값 분해 (0) | 2021.04.30 |
|---|---|
| [데이터 사이언스 스쿨] math 3.2 좌표와 변환 (0) | 2021.04.30 |
| [데이터 사이언스 스쿨] math 2.2 벡터와 행렬의 연산 (0) | 2021.04.30 |
| [데이터 사이언스 스쿨] math 2.1 데이터와 행렬 (0) | 2021.04.30 |
| [데이터 사이언스 스쿨] 5.5 Pandas의 시각화 기능 (0) | 2021.04.29 |



