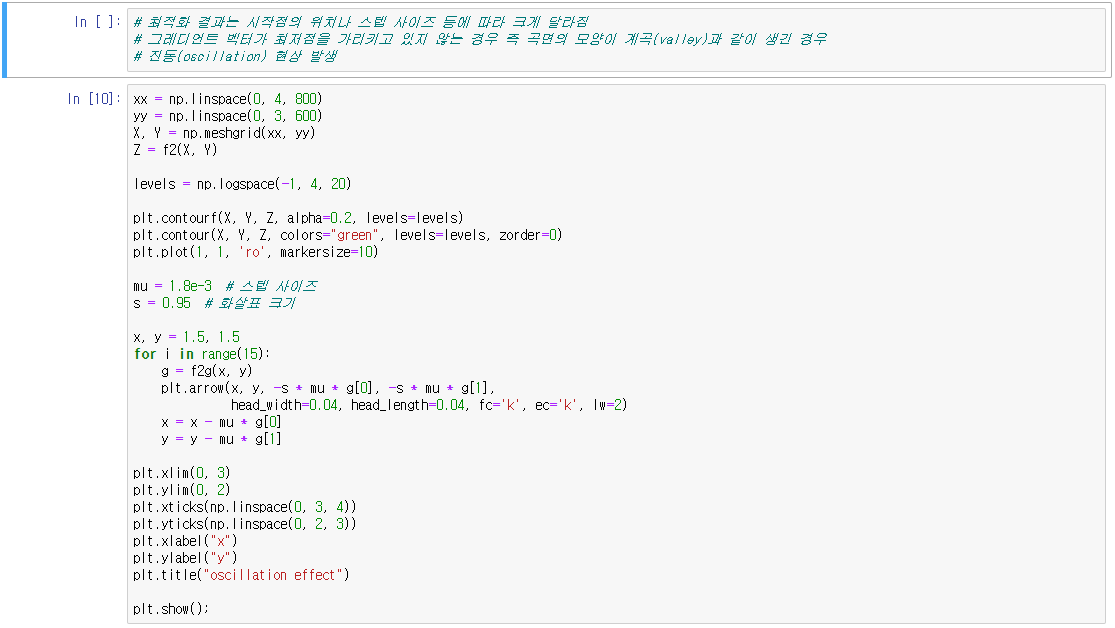
최적화 문제는 함수 f의 값을 최대화 혹은 최소화하는 변수 x의 값 x* 를 찾는 것
이 값 x*를 최적화 문제의 해(solution)라고 한다.


● 그리드 서치(grid search)와 수치적 최적화(numerical optimization)
- 그리드 서치 : 목적함수의 값을 가장 작게 하는 x의 위치를 찾기 위하여 가능한 x의 값을 여러개 넣어 보고 그중 가장 작은 값을 선택하는 것
- 수치적 최적화 : 반복적 시행 착오(trial and error)에 의해 최적화 필요조건을 만족하는 값 x*을 찾는 방법
수치적 최적화 방법은 다음 두 가지 알고리즘을 요구한다.
- 현재 위치 xkxk가 최적점인지 판단하는 알고리즘
- 어떤 위치 xkxk를 시도한 뒤, 다음 번에 시도할 위치 xk+1xk+1을 찾는 알고리즘







● 2차 도함수를 사용한 뉴턴 방법
- 뉴턴(newton) 방법 : 목적함수가 2차 함수라는 가정하에 한 번에 최저점을 찾는다. 그레디언트 벡터에 헤시안 행렬의 역행렬을 곱해서 방향과 거리가 변형된 그레디언트 벡터를 사용한다.
스텝 사이즈가 필요없고 목적함수가 실제로 2차함수와 비슷한 모양이면 빨리 수렴할 수 있다는 장점이 있지만 1차 도함수(그레디언트 벡터)뿐 아니라 2차 도함수(헤시안 행렬)도 필요로 한다.
● 준 뉴턴 방법
사람이 구한 헤시안 행렬 함수를 사용하는 대신 현재 시도하고 있는 xn 주변의 몇몇 점에서 함수의 값을 구하고 이를 이용하여 2차 도함수의 근사값 혹은 이에 상응하는 정보를 수치적으로 계산하는 방법
● SciPy를 이용한 최적화
사이파이(SciPy)의 optimize 서브 패키지는 최적화 명령 minimize()를 제공한다. 세부적인 알고리즘은 method 인수로 선택할 수 있다. 디폴트 알고리즘은 BFGS(Broyden–Fletcher–Goldfarb–Shanno) 방법이다.



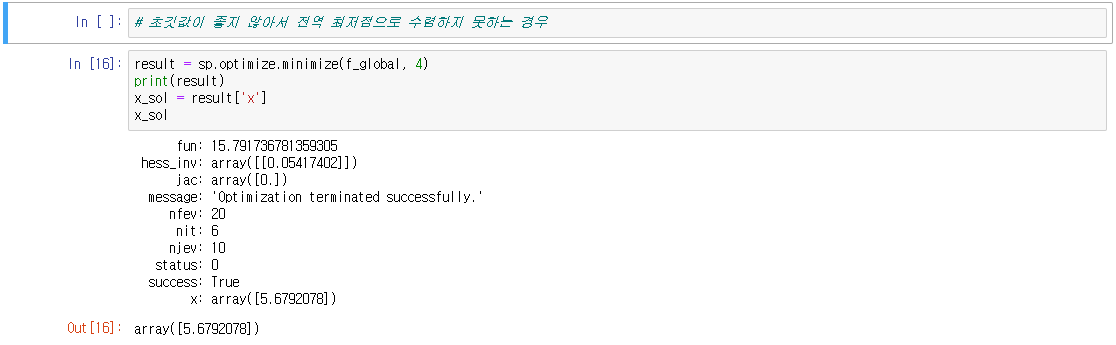
● 전역 최적화 문제
만약 최적화하려는 함수가 복수의 국소 최저점(local minima)을 가지고 있는 경우에는 수치적 최적화 방법으로 전역 최저점(global minimum)에 도달한다는 보장이 없다. 결과는 초기 추정값 및 알고리즘, 파라미터 등에 의존한다.


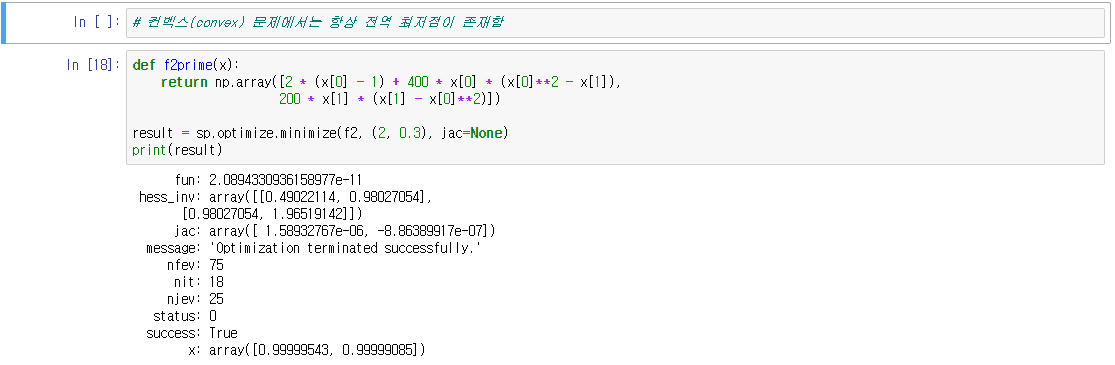
● 컨벡스(convex) 문제
목적함수의 2차 도함수의 값이 항상 0 이상이 되는 영역에서만 정의된 최적화 문제
다변수 목적함수의 경우에는 주어진 영역에서 헤시안 행렬이 항상 양의 준정부호(positive semidefinite)이라는 조건이 된다.
'IT 와 Social 이야기 > Python' 카테고리의 다른 글
| [데이터 사이언스 스쿨] math 5.3 선형계획법 문제와 이차계획법 문제 (0) | 2021.05.03 |
|---|---|
| [데이터 사이언스 스쿨] math 5.2 제한조건이 있는 최적화 문제 (0) | 2021.05.03 |
| [데이터 사이언스 스쿨] math 4.5 변분법 (0) | 2021.05.03 |
| [데이터 사이언스 스쿨] math 4.4 행렬의 미분 (0) | 2021.05.03 |
| [데이터 사이언스 스쿨] math 4.3. 적분 (0) | 2021.05.03 |



