
위의 그림에서 CONV는 합성곱 연산을 의미하고, 합성곱 연산의 결과가 활성화 함수 ReLU를 지남. 이 두 과정을 합성곱층(Convolution layer)이라고 함. 그 후에 POOL이라는 구간을 지나는데 이는 풀링 연산을 의미하며 풀링층(Pooling layer)이라고 함.
1. 합성곱 신경망의 대두
- 이미지를 다층 퍼셉트론을 이용하여 분류 시 이미지를 1차원 텐서인 벡터로 변환하여 다층 퍼셉트론의 입력층으로 사용하는데 이 1차원으로 변환된 결과는 변환 전에 가지고 있던 이미지의 공간적인 구조(spatial structure) 정보가 유실된 상태임
- 여기서 공간적인 구조 정보라는 것은 거리가 가까운 어떤 픽셀들끼리는 어떤 연관이 있고, 어떤 픽셀들끼리는 값이 비슷하거나 등을 포함하고 있음. 결국 이미지의 공간적인 구조 정보를 보존하면서 학습할 수 있는 방법이 필요해졌고, 이를 위해 사용하는 것이 합성곱 신경망임
2. 채널(Channel)
- 이미지는 '높이, 너비, 채널'의 3차원 텐서
- 높이 : 이미지의 세로 방향 픽셀 수
- 너비 : 이미지의 가로 방향 픽셀 수
- 채널(깊이 depth) : 색 성분(흑백:1, 컬러: 3)
3. 합성곱 연산(Convolution operation)
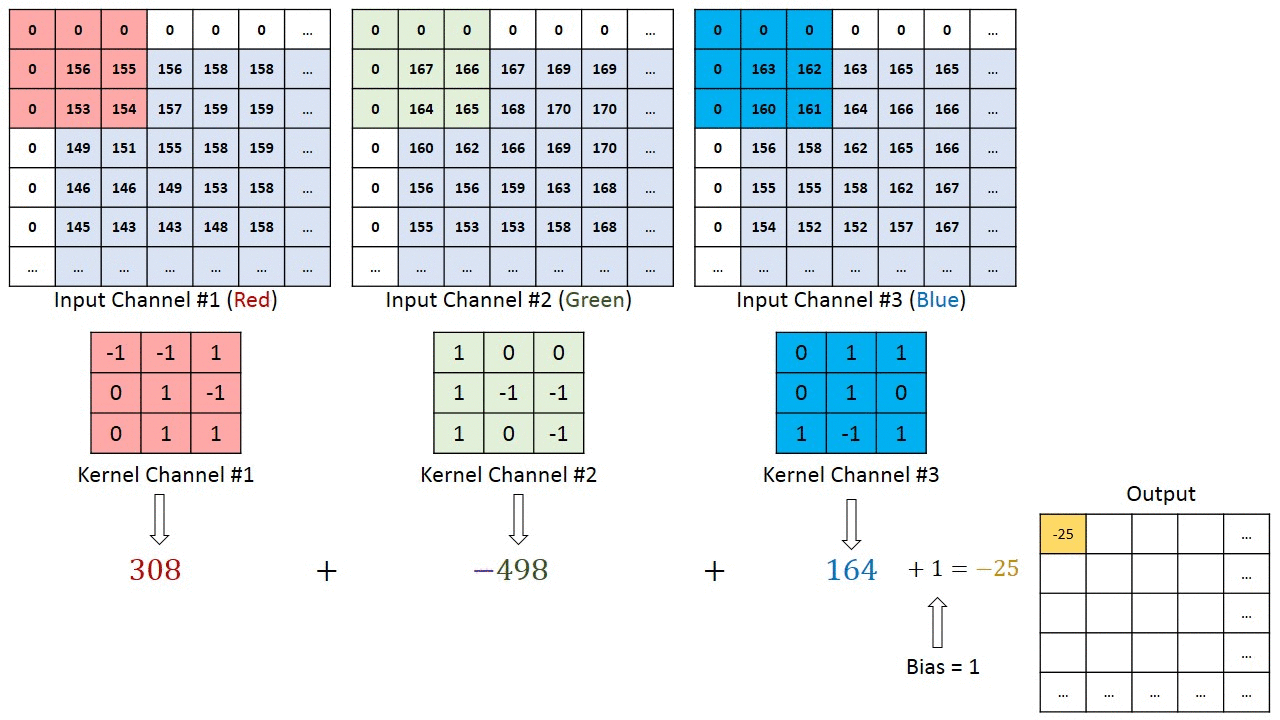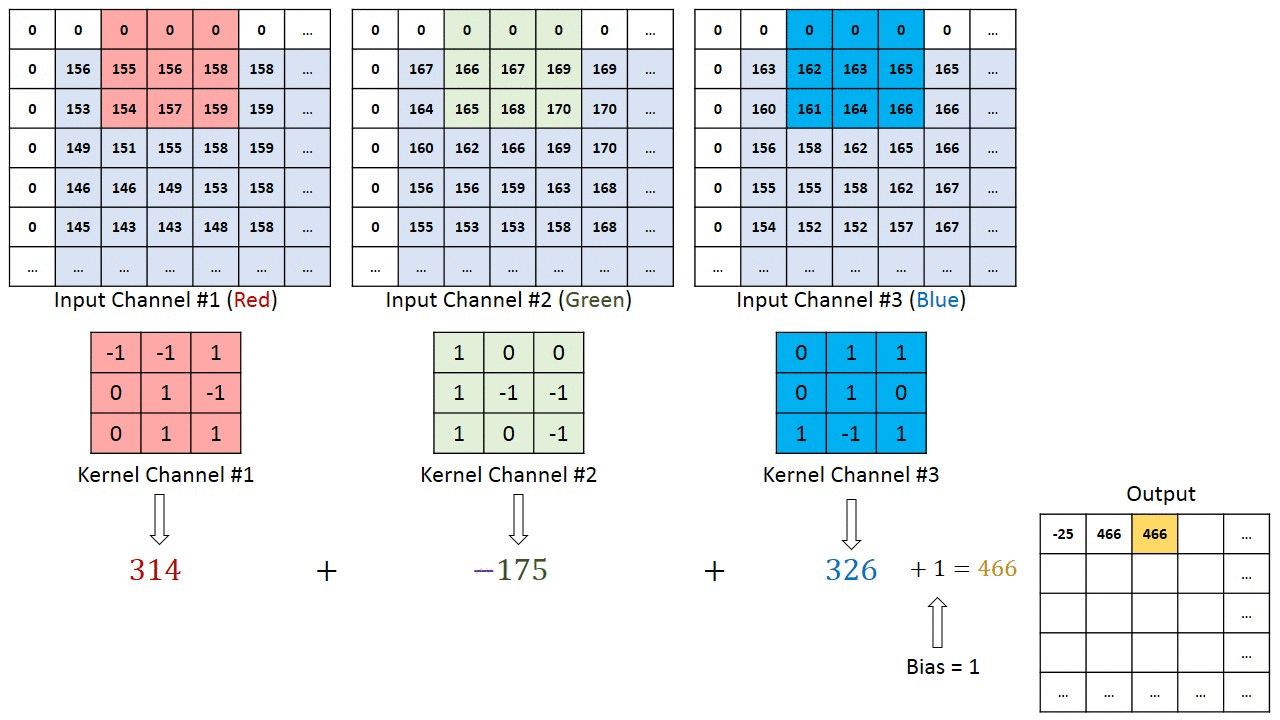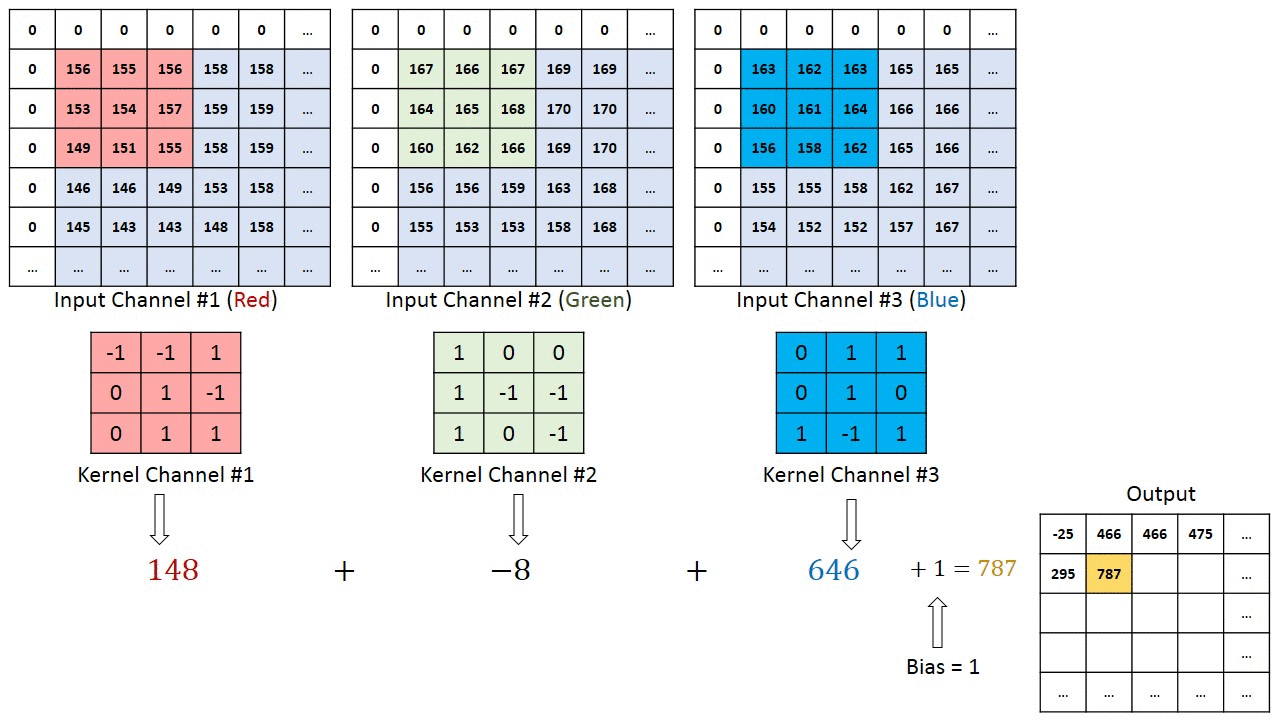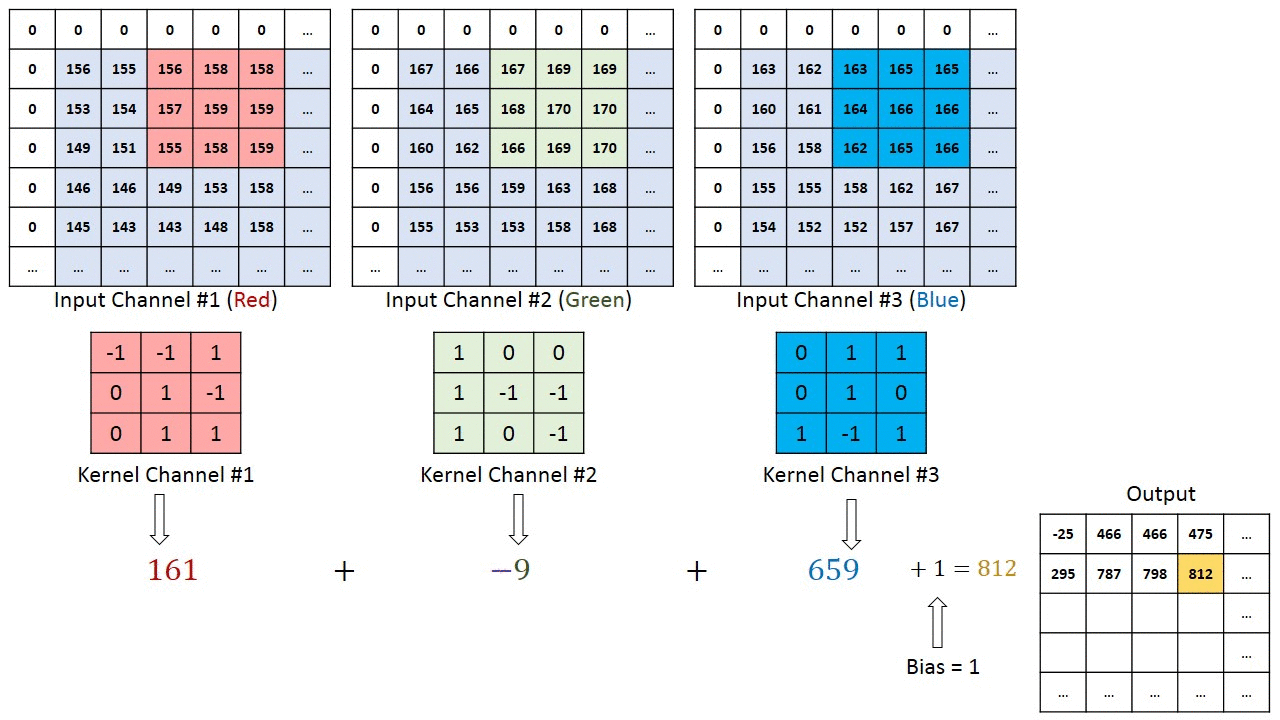
- 합성곱층(convolution layer)은 합성곱 연산을 통해 이미지의 특징을 추출 함
- 커널(kernel) 또는 필터(filter)라는 n×m 크기의 행렬로 높이(height)×너비(width) 크기의 이미지를 처음부터 끝까지 겹치며 훑으면서 n×m크기의 겹쳐지는 부분의 각 이미지와 커널의 원소의 값을 곱해서 모두 더한 값을 출력으로 하는 것
- 특성 맵(feature map) : 입력으로부터 커널을 사용하여 합성곱 연산을 통해 나온 결과
4. 패딩(Padding)
- 합성곱 연산의 결과로 얻은 특성 맵은 입력보다 크기가 작아진다는 특징이 있음
- 합성곱 연산 이후에도 특성 맵의 크기가 입력의 크기와 동일하게 유지할 필요가 있다면 패딩(padding)을 사용
- 패딩은 (합성곱 연산을 하기 전에) 입력의 가장자리에 지정된 개수의 폭만큼 테두리를 추가(0 패딩 등)
5. 가중치와 편향
- 합성곱 신경망의 가중치
- 커널 행렬의 원소
- 커널과 맴핑되는 픽셀만을 입력으로 사용하므로 다층 퍼셉트론을 사용할 때보다 훨씬 적은 수의 가중치를 사용하여 공간적 구조 정보를 보존
- 합성곱 신경망의 편향
- 하나의 값만 존재, 커널이 적용된 결과의 모든 원소에 더해짐
6. 특성 맵의 크기 계산 방법
- 입력의 크기와 커널의 크기, 그리고 스트라이드의 값만 알면 합성곱 연산의 결과인 특성 맵의 크기를 계산할 수 있음
7. 다수의 채널을 가질 경우의 합성곱 연산
- 커널의 채널 수도 입력의 채널 수만큼 존재해야 함 즉, 입력 데이터의 채널 수와 커널의 채널 수는 같아야 함
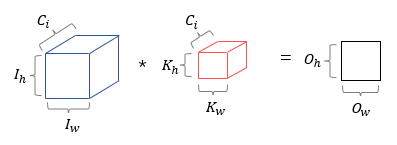
8. 3차원 텐서의 합성곱 연산
- Ih : 입력의 높이
- Iw : 입력의 너비
- Kh : 커널의 높이
- Kw : 커널의 너비
- Oh : 특성 맵의 높이
- Ow : 특성 맵의 너비
- Ci : 입력 데이터의 채널
9. 풀링(Pooling)
- 풀링층(Pooling layer)에서는 특성 맵을 다운샘플링하여 특성 맵의 크기를 줄이는 풀링 연산이 이루어 짐
- 최대 풀링(max pooling)과 평균 풀링(average pooling)이 있음
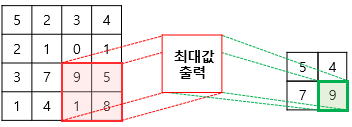
- 출처 : [딥러닝을이용한 자연어 처리 입문] 1201 합성곱 신경망(Convolution Neural Network)
'IT 와 Social 이야기 > NLP 자연어처리' 카테고리의 다른 글
| [딥러닝을이용한 자연어 처리 입문] 1203 1D CNN으로 IMDB 리뷰 분류하기 (0) | 2021.05.26 |
|---|---|
| [딥러닝을이용한 자연어 처리 입문] 1202 자연어 처리를 위한 1D CNN(1D Convolution Neural Network) (0) | 2021.05.26 |
| [온라인새벽기도] 하나님 손에 붙들리라 (0) | 2021.05.26 |
| [딥러닝을이용한 자연어 처리 입문] 1108 BiLSTM으로 한국어 스팀 리뷰 감성 분류하기 (0) | 2021.05.25 |
| [딥러닝을이용한 자연어 처리 입문] 1107 네이버 쇼핑 리뷰 감성 분류하기(Naver Shopping Review Sentiment Analysis) (0) | 2021.05.25 |



