[데이터 사이언스 스쿨] math 4.1 함수

● 함수(function)

 

함수(function)는 입력 값을 출력 값으로 바꾸어 출력하는 관계(relationship)를 말한다. 맵(map), 매핑(mapping), 또는 딕셔너리(dictionary)이라는 용어를 사용하기도 한다.

 

어떤 입력 값과 출력 값이 함수 관계를 이루기 위해서는 같은 입력 값에 대해서 항상 같은 출력 값이 나와야 한다.

 

[ 이미지 출처 : tcpschool.com - 함수 ]

 

 

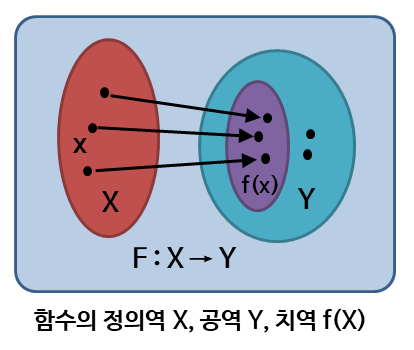
함수에서 입력변수가 가질 수 있는 값의 집합을 정의역(domain), 출력변수가 가질 수 있는 값의 집합을 공역(range)이라고 한다.

 

 

 

● 연속과 불연속

 

함수의 값이 중간에 갑자기 변하는 것을 불연속(discontinuous)이라고 하고 그렇지 않으면 연속(continuous)이라고 한다.

 

 

● 지시 함수(indicator function)

 

함수 이름에 아래 첨자로 미리 지정된 값이 들어오면 출력이 1이 되고 아니면 출력이 0이 된다.

 

지시함수는 데이터 중에서 특정한 데이터만 선택하여 갯수를 세는데 사용된다.

 

 

● 역함수(inverse function)

 

어떤 함수의 입력/출력 관계와 정반대의 입출력 관계를 갖는 함수. 함수가 존재한다고 해서 항상 역함수가 존재할 수 있는 것은 아니다.

 

 

● 역함수의 그래프

 

역함수의 그래프는 원래의 함수에서 xx축과 yy축이 바뀐 것이므로 y=xy=x가 나타내는 직선(원점을 통과하는 기울기 1인 직선)을 대칭축으로 대칭인 함수의 그래프와 같다.

 

 

● 데이터 분석에서 많이 사용되는 함수들

 

- 다항식(polynomial) 함수: 거듭제곱 항의 선형조합으로 이루어진 함수다.

- 최대함수와 최소함수 : 최대함수는 두 개의 인수 중에서 큰 값을, 최소함수는 작은 값을 출력하는 함수

- 최대함수는 원래 두 개의 입력을 갖는 함수이지만 보통 y=0으로 고정해서 입력값 x가 양수이면 그대로 출력하고 음수일 때는 0으로 만들 때 주로 사용한다.

 

 

- 지수(exponential) 함수 : 거듭 제곱의 밑을 오일러 수 e(약 2.718)로 하여 거듭제곱을 하는 함수

 

 

- 지수 함수의 특성

 

• 양수(e)를 거듭제곱한 값이므로 항상 양수다.
• x=0일 때 1이 된다.
• x가 양의 무한대로 가면(x→∞), 양의 무한대로 다가간다.
• x가 음의 무한대로 가면(x→−∞), 0으로 다가간다.
• x1>x2이면 expx1>expx2 이다.

 

 

- 로지스틱(logistic) 함수 : 지수함수를 변형한 함수. 시그모이드(sigmoid) 함수라는 종류의 하나. 로지스틱함수가 가장 널리 쓰이기 때문에 보통 시그모이드 함수라고 하면 이 로지스틱함수를 뜻한다.

 

 

- 로그(log) 함수 : 지수 e를 거듭제곱하여 특정한 수 a가 되도록 하는 수를 log⁡ a라 표기하고 로그(log)라고 읽는다.

 

 

 

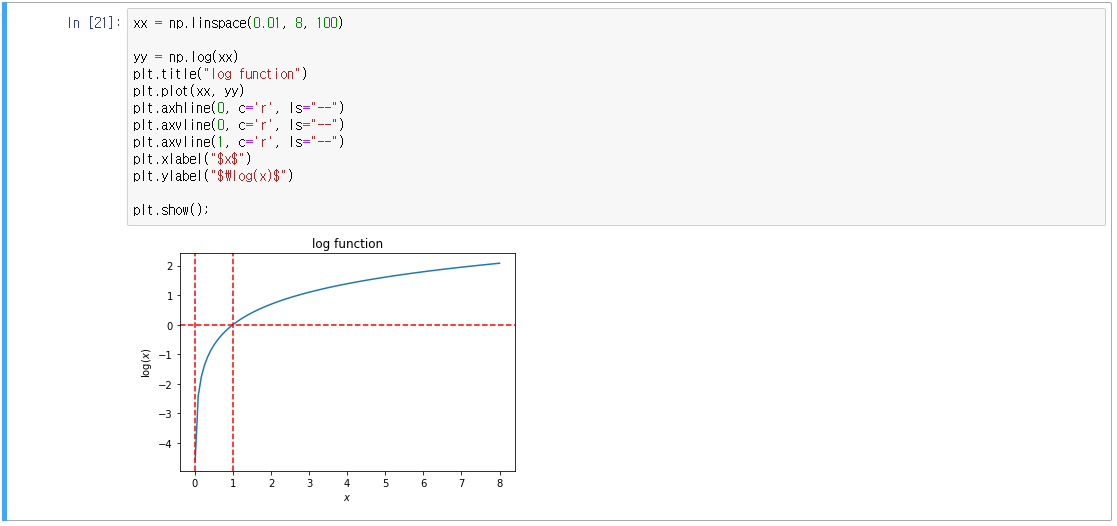
- 로그 함수의 특징

 

• x값, 즉 입력변수값이 양수이어야 한다. 0이거나 음수이면 정의되지 않는다.
• x>1x 이면 y>0 (양수)
• x=1x 이면 y=0
• 0<x<1 이면 y<0 (음수)
• x1>x2 이면 logx1>logx2 이다.

 

 

● 로그 함수의 성질

 

- 로그함수는 곱하기를 더하기로 변환한다.

- 어떤 함수에 로그를 적용해도 함수의 최고점, 최저점의 위치는 변하지 않는다.

- 로그함수는 0부터 1사이의 작은 값을 확대시켜 보여준다. (로그함수는 0부터 1사이의 구간을 음의 무한대부터 0까지로 확장시켜주기 때문에 확률값처럼 0과 1사이에 있는 작은 값을 더 확실하게 비교할 수 있도록 한다.)

 

 

- 소프트플러스(softplus) 함수 : 지수함수와 로그함수를 결합하여 만든 함수로 0을 인수로 갖는 최대함수와 비슷하지만 x=0 근처에서 값이 부드럽게 변한다는 장점이 있다.

 

 

- 다변수(multivariate) 함수 : 복수의 입력변수를 갖는 함수

 

 

- 분리가능(separable) 다변수 함수 : 단변수함수의 곱으로 표현 가능한 다변수함수

 

 

- 다변수 다출력 함수 : 출력변수도 여러개일 수 있다. 이 경우에는 출력을 벡터나 행렬로 나타낼 수 있다. 소프트맥스(softmax)함수는 다차원 벡터를 입력받아 다차원 벡터를 출력한다.

 

출력 벡터는 다음과 같은 특성을 갖는다.

• 모든 출력 원소는 0와 1 사잇값을 갖는다.
• 모든 출력 원소의 합은 1이다.
• 입력 원소의 크기 순서와 출력 원소의 크기 순서가 같다.

 

 

 

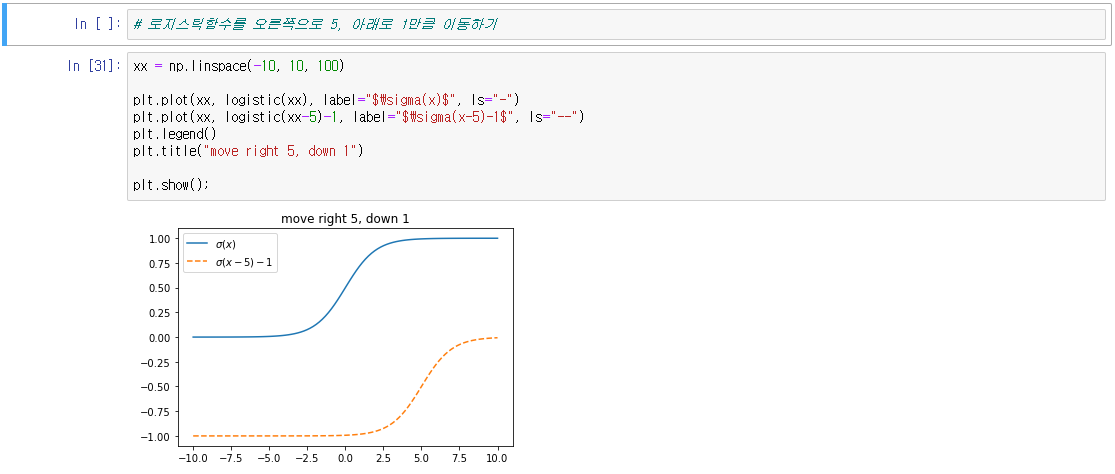
● 함수의 평행이동

 

 

● 함수의 스케일링

 

 

 

dss_math4_1_function.ipynb

0.44MB

 

 

- 출처 : [데이터 사이언스 스쿨] math 4.1 함수